Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model?

Yang Yue1*† Zhiqi Chen1* Rui Lu1 Andrew Zhao1 Zhaokai Wang2 Yang Yue1 Shiji Song1 and Gao Huang1‡
1 Tsinghua University, LeapLab    2 Shanghai Jiao Tong University
* Equal Contribution    † Project Lead    ‡ Corresponding Author
Correspond to: {le-y22,zq-chen23}@mails.tsinghua.edu.cn , gaohuang@tsinghua.edu.cn
Paper arXiv GitHub

Yang Yue is currently focused on developing new paradigms for incentivizing LLM/MLLM reasoning, generalized world models, and exploring the generalization of VLA. He is seeking active collaboration opportunities with companies that offer the freedom to explore these frontier and fundamental questions, alongside abundant resources and a strong technical atmosphere. Additionally, he is seeking a Ph.D. visit. Please feel free to reach out if there is potential for collaboration.

Video: pass@k curves of base models and their zero-RL-trained counterparts across multiple mathematical benchmarks.
When k is small, RL-trained models outperform their base versions. However, as k increases to the tens or hundreds,
base models consistently catch up with RL-trained models across all benchmarks and LLM families without exception.
Eventually, base models surpass RL-trained models.

Introducing Our Work

Recent breakthroughs in reasoning-focused large language models (LLMs) like OpenAI-o1, DeepSeek-R1, and Kimi-1.5 have largely relied on Reinforcement Learning with Verifiable Rewards (RLVR), which replaces human annotations with automated rewards (e.g., verified math solutions or passing code tests) to scale self-improvement. While RLVR enhances reasoning behaviors such as self-reflection and iterative refinement, we challenge a core assumption:

Does RLVR actually expand LLMs' reasoning capabilities, or does it merely optimize existing ones?

By evaluating models via pass@k, where success requires just one correct solution among k attempts, we uncover that RL-trained models excel at low k (e.g., pass@1) but are consistently outperformed by base models at high k (e.g., pass@256). This demonstrates that RLVR narrows the model's exploration, favoring known high-reward paths instead of discovering new reasoning strategies. Crucially, all correct solutions from RL-trained models already exist in the base model's distribution, proving RLVR enhances sampling efficiency, not reasoning capacity, while inadvertently shrinking the solution space.

Video: The effect of RLVR on LLM's reasoning ability. Search trees are generated by repeated sampling from the base and
RLVR-trained models for a given problem. Grey indicates paths that are unlikely to be sampled by the model, while black
indicates paths that are likely to be sampled. Green indicates correct paths, which has positive rewards.
Our key finding is that all reasoning paths in the RLVR model are already present in the base model.
For certain problems like Problem A, RLVR training biases the distribution toward rewarded paths, improving sampling
efficiency. However, this comes at the cost of reduced scope of reasoning capacity: For other problems like Problem B,
the base model contains the correct path, whereas that of the RLVR model does not.

Conclusion

  1. RL-trained models perform worse than base models in pass@k at large k values.
    While RL-trained models outperform base models at low sampling sizes (small k), base models consistently surpass them at larger k across all benchmarks, even achieving higher pass@k scores. Manual inspection reveals that base models can solve problems thought to require RL training by generating diverse reasoning paths, with at least one correct solution per problem. This indicates that RL training does not enhance—and may even limit—the full reasoning potential of LLMs compared to aggressive sampling in the base model.
  2. RL boosts sampling efficiency but reduces the reasoning capacity boundary.
    The analysis reveals that RLVR-trained models generate reasoning paths already within the base model's output distribution, meaning RLVR biases the model toward higher-rewarded solutions rather than creating entirely new reasoning abilities. However, this focus on rewarded paths reduces the model's exploration capacity, limiting its coverage of solvable problems at larger sampling sizes. These findings suggest that RLVR does not fundamentally transcend the base model's reasoning capabilities but instead optimizes existing pathways at the cost of broader problem-solving diversity.
  3. RLVR algorithms perform similarly and remain far from optimal.
    The study compares various RL algorithms (PPO, GRPO, Reinforce++) and finds their performance differences minor, as measured by the sampling efficiency gap (∆SE), which assesses how close they get to optimal sampling efficiency. Despite slight variations in ∆SE among algorithms, the gap remains large across all methods. This indicates that current RL approaches, focused on improving sampling efficiency, still fall far short of optimal performance.
  4. RLVR and distillation are fundamentally different.
    While RL improves sampling efficiency, distillation can genuinely introduce new knowledge into the model. As a result, distilled models often exhibit an expanded scope of reasoning capability beyond that of the base model by learning from distilled models, in contrast to RLVR-trained models whose capacity remains bounded by the base.

Q&A

01 Q

You're using pass@k instead of majority vote—doesn't that make the results invalid?

A

[1/3] We use pass@k not to measure practical utility, but to explore the reasoning capacity boundary of LLMs, as outlined in our paper.
[2/3] If a model can solve a difficult problem at least once in k samples, we consider that problem within its potential reasoning scope. If RL training truly expands reasoning, we would expect the RL model to solve more such problems than the base.
[3/3] However, we observe the opposite: RLVR models often solve fewer problems at large k, suggesting a narrowing of this boundary. This implies RLVR is optimizing within the base model's capabilities, not extending them.

02 Q

Isn't pass@k meaningless since you could eventually guess the right answer through randomly sampling k times?

A

[1/3] It's true that pass@1024 can be noisy for datasets like AIME whose answers are within limited integer space. But we also evaluated coding benchmarks, where guessing is nearly impossible to pass unit test case, and yet similar patterns hold, with base models performing better at large k.
[2/3] For AIME and GSM8K, we manually inspected the CoT outputs and found that, in most cases, the base model produced at least one correct reasoning path—not just lucky guesses.
[3/3] On datasets usch MATH500, where answers involve complex forms (roots, fractions, symbolic math) and are hard to guess, we again observed similar trends.
Together, these results highlight the often underappreciated reasoning potential of base models. We're considering including a random sampling baseline in future work.

03 Q

Even random sampling can eventually generate the correct answer with a large enough k. So doesn't that make your result—that RL improves over base model's pass@k—meaningless?

A

Not quite. “More is different.” While it's true that in theory, even random typing has a non-zero chance of producing a correct answer—about 1/V^L, where V is the vocabulary size (~30k) and L is the output length (>200). However, in practice, that search space is astronomically large.
The key point is that the magnitude of that probability matters. If the base model has a prior that gives the correct answer a 1 in 10⁴ or 10⁵ chance, then RL might find it with millions of samples. But if that probability is 1 in 10¹⁰ or smaller, RL is extremely unlikely to escape local optima and reach meaningful reward.
In our paper, we show that for most problems, this probability is not negligible—we observe correct outputs with k = 128 or 1024, which is feasible with today's resources. So rather than being meaningless, pass@k reveals that base models already possess the necessary reasoning paths.

04 Q

Isn't it common sense that RL should turn pass@k into pass@1?

A

It's not surprising that RLVR turns pass@k into pass@1—that's what RL is designed for.
But what's more interesting is that RLVR doesn't do much beyond that in our experiments. It doesn't seem to introduce new reasoning abilities: if the base model can't solve a problem, the RL-trained model still can't either. This clearly highlights the upper bound of RL in reasoning.
And that's not something obvious. In traditional RL such as Atari or Go, RL is known to explore and discover new strategies, continuously self-improving without an inherent bound. But in the case of LLMs, RLVR seems constrained by the base model's existing capabilities.
Actually, this phenomenon that RL-trained models perform worse than base models in pass@k surprises lots of researchers.

05 Q

Does your paper claim that RL can't incentivize reasoning beyond the base model?

A

No, we're not making such a strong claim. Our goal is to present systematic experiments and analyses to explore the question: "Does RL truly expand reasoning capacity in LLMs?" and hope bring some new insights for the community.
We don't rule out the possibility that scaling up model size and training data could change the outcome. In fact, we're currently working on DeepSeek-V3-base vs. R1-zero to investigate this further.

06 Q

Is your paper saying RL is useless?

A

No. RL remains practically useful because it improves sample efficiency. However, if we want LLMs to solve truly harder problems beyond pretraining, we may need a new training paradigm that can go beyond the base model's ceiling.

07 Q

DeepSeek-Math reported similar results. How is your work different?

A

Yes, DS-Math did observe similar trends, but their study was limited to a single instruction-tuned model and two math benchmarks.
In contrast, Our work systematically investigates this across true base models in a zero-RL setting, covering multiple LLM families and a wider range of benchmarks.
We also dive further by providing deeper analyses—including perplexity trends, different RL algorithms, and evaluation against distilled models—offering a more comprehensive view of RLVR's capabilities and limitations.
We believe the fact that the reasoning scope of RLVR models is bounded by the base model is a notable phenomenon that deserves deeper attention.

Experiments

We conducted experiments across three representative domains to evaluate the effect of RLVR on the reasoning ability boundaries of base and RLVR models.

Math

In the math experiments, we evaluate multiple LLM families (Qwen-2.5 and LLaMA-3.1) and their RL-trained variants on benchmarks like GSM8K, MATH500, and AIME24. We analyze pass@k curves to compare base and RL-trained models, observing that RL improves low-k performance but reduces problem coverage at high k. We manually inspect CoT validity to ensure correct answers stem from valid reasoning, not lucky guesses. Additionally, we examine Oat-Zero-trained models and filter guessable problems to focus on challenging cases. The results show base models maintain broader reasoning coverage despite RL's initial accuracy gains.

Coding

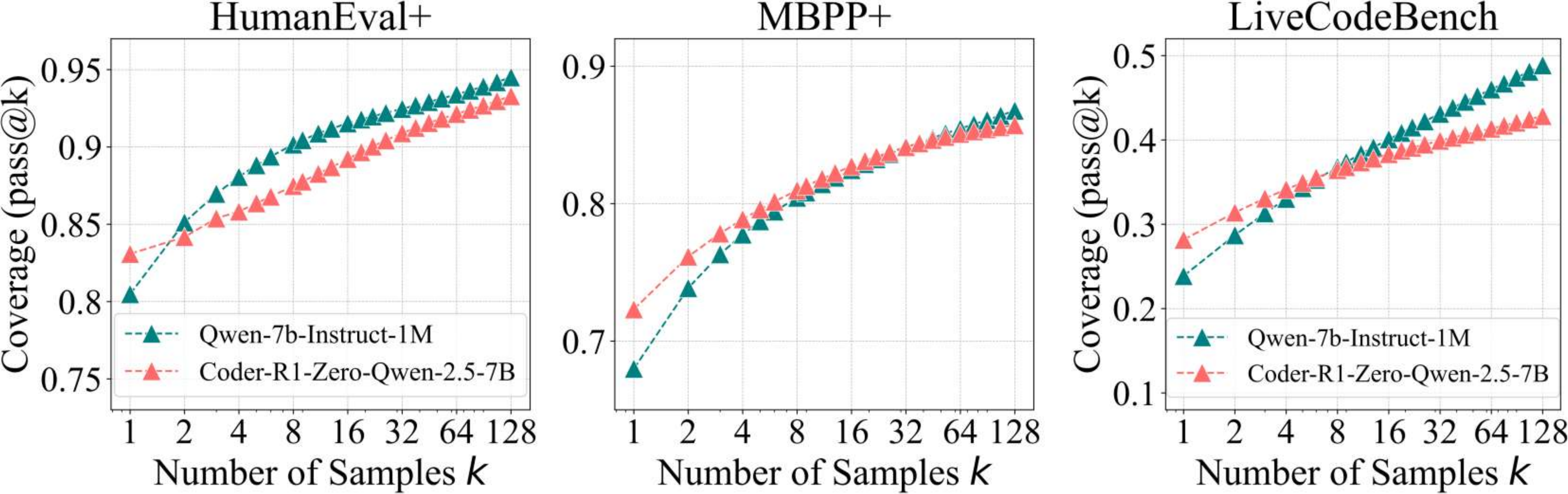
In the coding experiments, we evaluate the RLVR-trained model CodeR1-Zero-Qwen2.5-7B, derived from Qwen2.5-7B-Instruct-1M, on benchmarks like LiveCodeBench, HumanEval+, and MBPP+. We assess performance using pass@k metrics, measuring correctness based on predefined test cases. The results show RLVR improves single-sample pass@1 scores but reduces coverage at higher sampling counts (k = 128). The original model exhibits continued potential for improvement with larger k, while RLVR's performance plateaus. This indicates RLVR enhances deterministic accuracy but limits exploration diversity.

Visual Reasoning

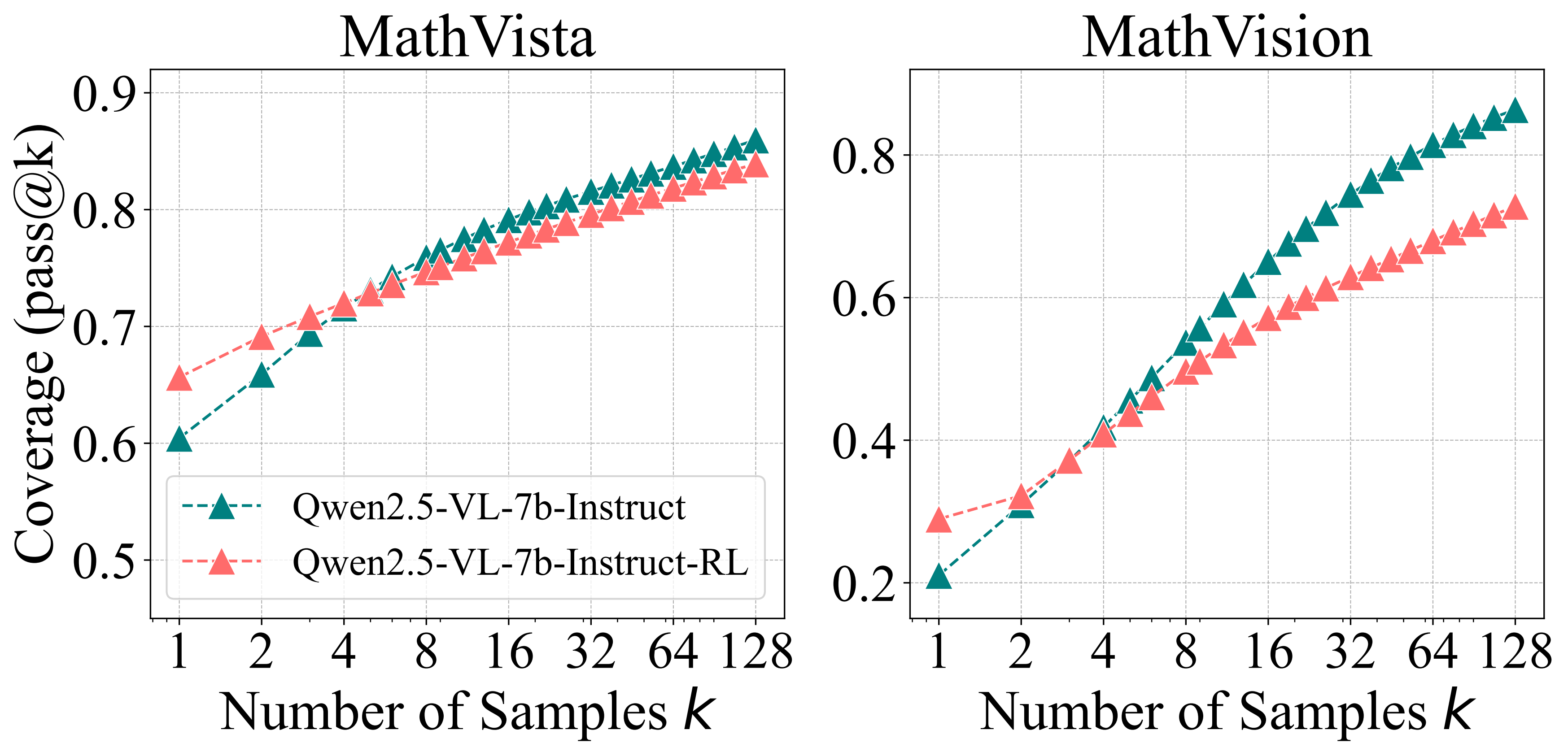
In the experiments on visual reasoning, we evaluate Qwen-2.5-VL-7B on filtered visual reasoning benchmarks (MathVista and MathVision), removing multiple-choice questions to focus on robust problem-solving. The improvements from RLVR in visual reasoning align with those seen in math and coding benchmarks, indicating that the original model already covers a broad range of solvable problems, even in multimodal tasks. The consistency across domains suggests that RLVR enhances reasoning capabilities without fundamentally altering the model's problem-solving approach.

Case Study

We present ONE of the sampled correct CoTs from the base model, manually selected from 2048 samplings for the hardest questions in AIME24. The responses from the base model tend to be long CoTs and exhibit reflective behavior, highlighting the strong reasoning ability inherent in the base model.

Example

BibTeX

@article{yue2025limit-of-rlvr,
  title={Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model?},
  author={Yue, Yang and Chen, Zhiqi and Lu, Rui and Zhao, Andrew and Wang, Zhaokai and Yue, Yang and Song, Shiji and Huang, Gao},
  journal={arXiv preprint arXiv:2504.13837},
  year={2025}
}